リチウムイオンバッテリモデルをSimulink®で作ってみた 【第3回】SOCを変数とする近似式でEocv, R, Cを表現するモデル編

このTECHブログでは、自動車業界で普及してきているモデルベース開発を用いて、リチウムイオンバッテリの評価を効率的に行うことができるモデルを作成します。
このモデル作成には、MathWorks社のSimulink®を使用して作成します。
複数回にわたり、様々なタイプのモデルを作成します。最終的にはHDL Coderを使用してHDL化まで行うことを予定しています。
今回は第3回目でSOC(充電率)を変数とする近似式でOCV電圧、R、Cを表現するモデルを作成します。第2回で使用した、OCV電圧, R0, R1, C1のLookup TableからSOCを説明変数とする近似多項式を算出してモデルを作成し、Lookup Tableを使用した前回モデルとシミュレーション結果の比較を行います。
なお、実行した環境は以下の通りです。
| OS | Microsoft Windows 10 Pro |
|---|---|
| MathWorks社製 | MATLAB® バージョン 9.8 (R2020a) |
| Simulink® バージョン 10.1 (R2020a) |
目次
リチウムイオンバッテリの等価回路モデルと回路方程式
今回使用する等価回路モデルと回路方程式は第2回目で使用したものと同じものです。
ただ前回はLookup Tableを用いて表現していたOCV電圧、R、Cを、今回はSOCの変数として近似式で表現するため、Simulink®モデル作成時に差異がでてきます。
Lookup Tableを用いるか、近似式を用いるかは、精度やシミュレーションの速さ、HDL化したときの使用リソース量などで、メリット・デメリットを考えどちらを選択するかを決めます。また、次回以降にHDL化時の使用リソース量の比較を行う予定です。
SOCを変数とする近似式でEocv, R, Cなどを表現
前回モデルでEocv, R, CなどをLookup Tableで表していたものを、SOCを変数とする近似式で表現します。
今回、近似式の算出には、「MATLAB® の基本的な近似 UI 」※を使用しました。最高10次の多項式を用いて近似できます。低次数(2~6次)でよい場合は、Excelを使用して算出することも可能です。
使用したデータは図1の温度Tが293.15[K](=20℃)のデータです。
※詳細は以下を参照。
https://jp.mathworks.com/help/matlab/data_analysis/interactive-fitting.html#f1-15488
それでは、近似式を算出する手順を順番に見ていきます。
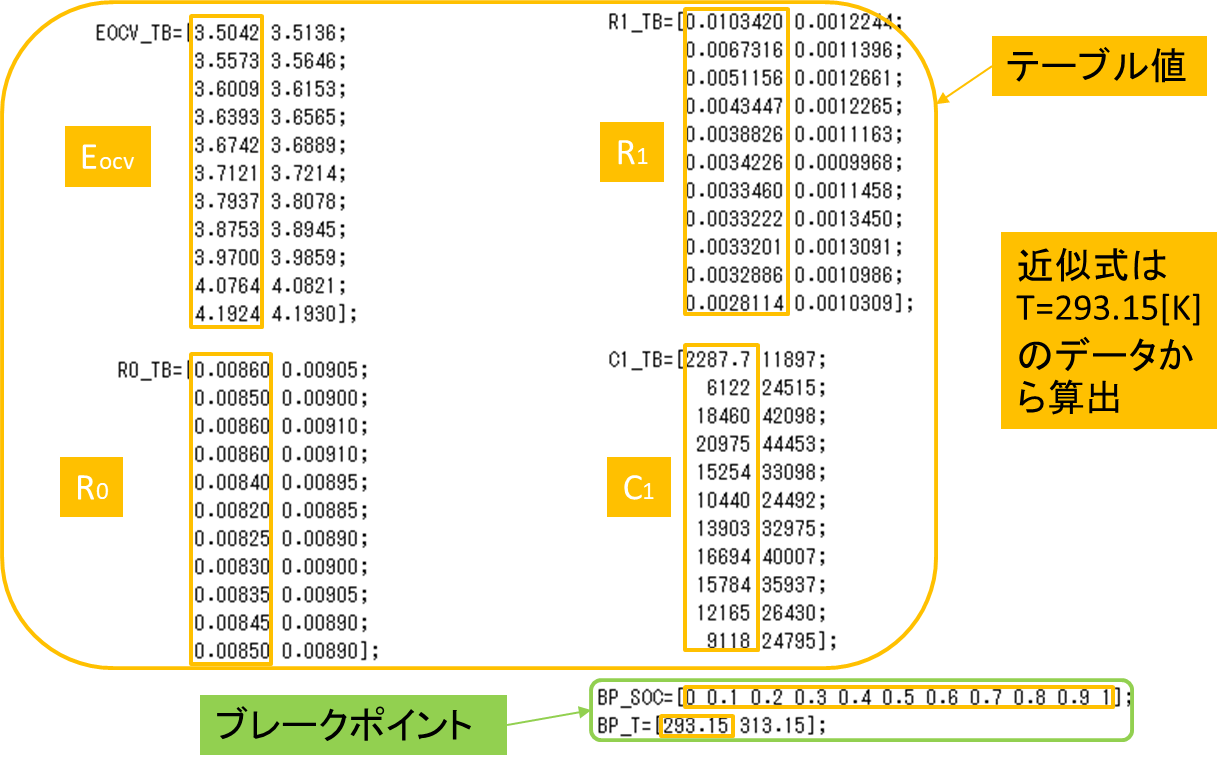
図1 Lookup Table値, ブレークポイント値
まず、図1のLookup Table値,ブレークポイント値をmファイルに保存し、実行してワークスペースに読込みます。
続いて読込んだデータの散布図を表示させます。以降はEocvの近似式を算出場合の手順です。R0,R1,C1の場合も同様の手順で算出できます。
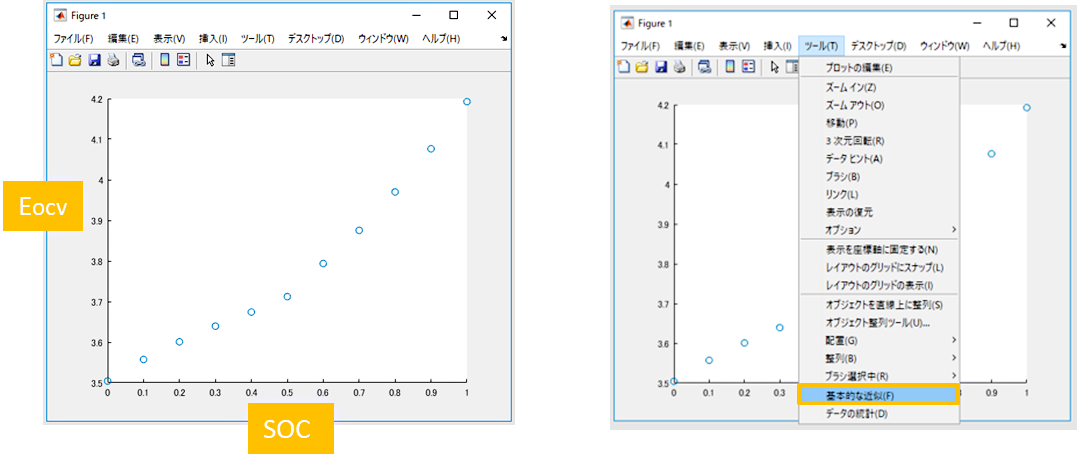
MATLABのコマンドウィンドウで以下のコマンドを入力すると、図2のようにFigureウィンドウ上に散布図が表示されます。図3のようにFigureウィンドウ上で「ツール(T)」―「基本的な近似(F)」を選択すると「基本的な近似UI」が起動します。
![]()
図2 プロット結果
図3「基本的な近似」UIを起動
※画像クリックで大きな画像が表示されます。
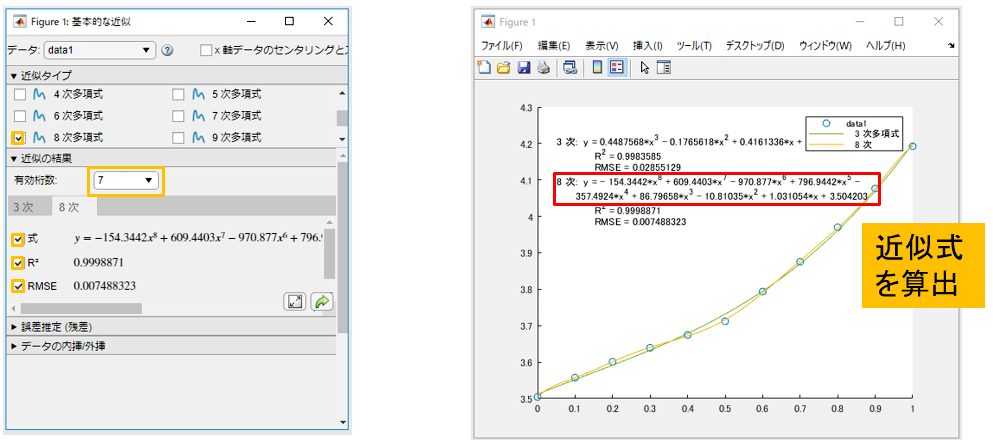
図4のように「基本的な近似UI」で「近似タイプ」欄から多項式の次数、「近似の結果」欄から有効桁数、式、R2、RMSEを設定すると、図5のように近似式でFittingされた結果が表示されます。
R2(決定係数),RMSE(二乗平均平方根誤差)は回帰分析で適合度合を評価する指標です。R2は0から1までの値をとり1に近いほど、RMSEは小さいほど近似式が実際のデータに当てはまっていることを表します。図5では比較のため、近似タイプ3次と8次の多項式の結果を表示させています。今回は、R2、RMSEの結果を比較して8次を選択しました。
図4「基本的な近似UI」
図5 近似曲線のFitting
※画像クリックで大きな画像が表示されます。
R0,R1,C1の場合も同様に近似式を算出し、図6に示した係数を求めました。

図6 近似式の係数
回路方程式をSimulink®モデルへ(SOCを変数とする近似式でEocv, R, Cなどを表現)
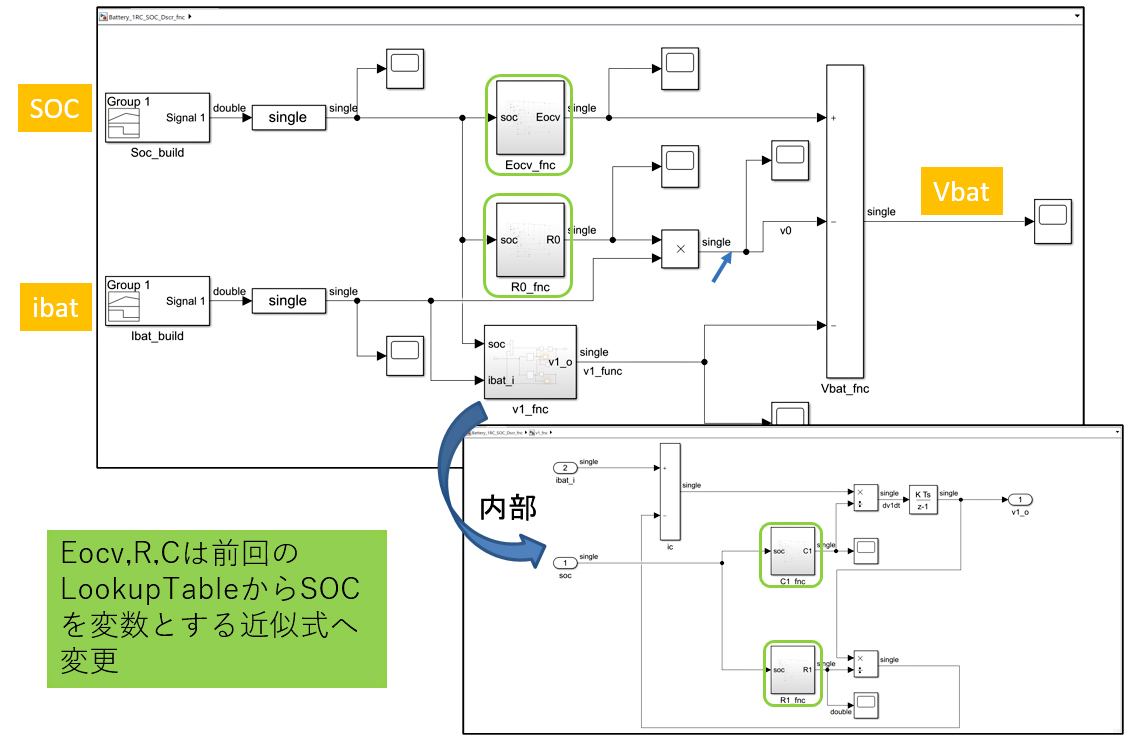
図7のようにSOC, ibatを入力、Vbatを出力とし、前回モデルでEocv, R, CをLookup Tableで表していたものを、SOCを変数とする近似式で表現する、Simulink®モデルに変更しました。
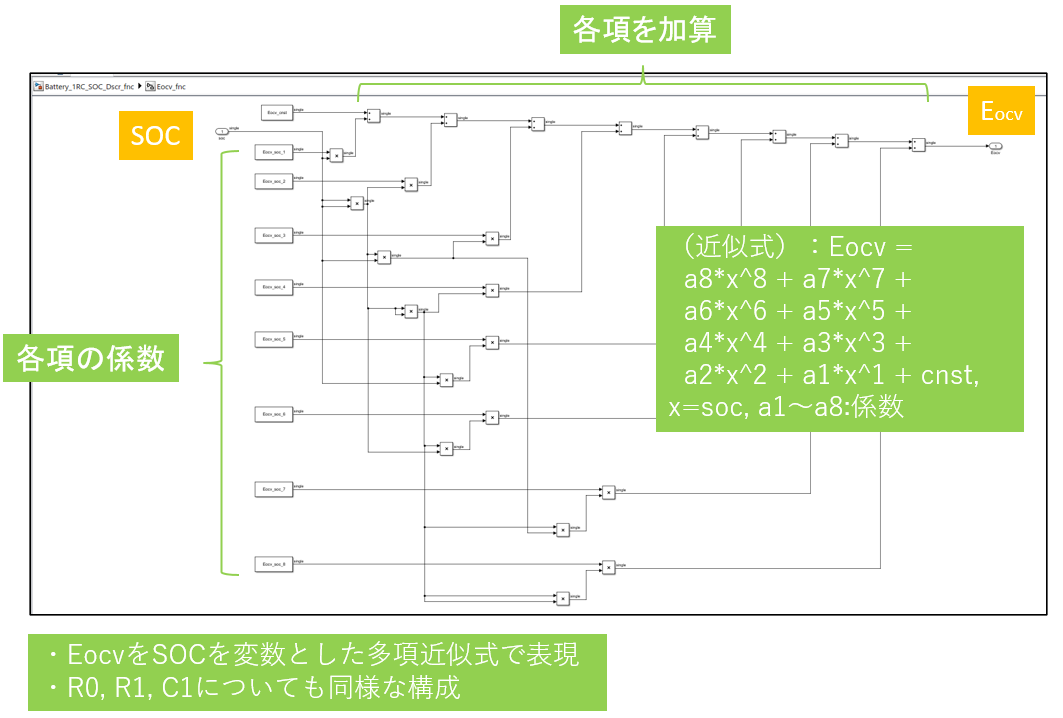
Eocvの近似多項式モデルが図8に示した通りです。先程求めた、8次の近似多項式をモデル化してあります。
図7 Eocv, R, CをSOCの関数で表した、リチウムイオンバッテリのSimulink®モデル
※画像クリックで大きな画像が表示されます。
図8 Eocvの近似多項式モデル
※画像クリックで大きな画像が表示されます。
シミュレーションによる評価
上記で作成した、近似式を使用したリチウムイオンバッテリのSimulink®モデルで、前回と同様に図9のようにSOCが1の状態からibat =5[A]で240[s]間放電した場合のVbatの変化をシミュレーションにより評価しました。最後に第2回のLookup Tableを使用したモデルとシミュレーション結果を比較しました。
ibat を0[A]から5[A]に変化するタイミングでSOCを1から0.9に変化させています。
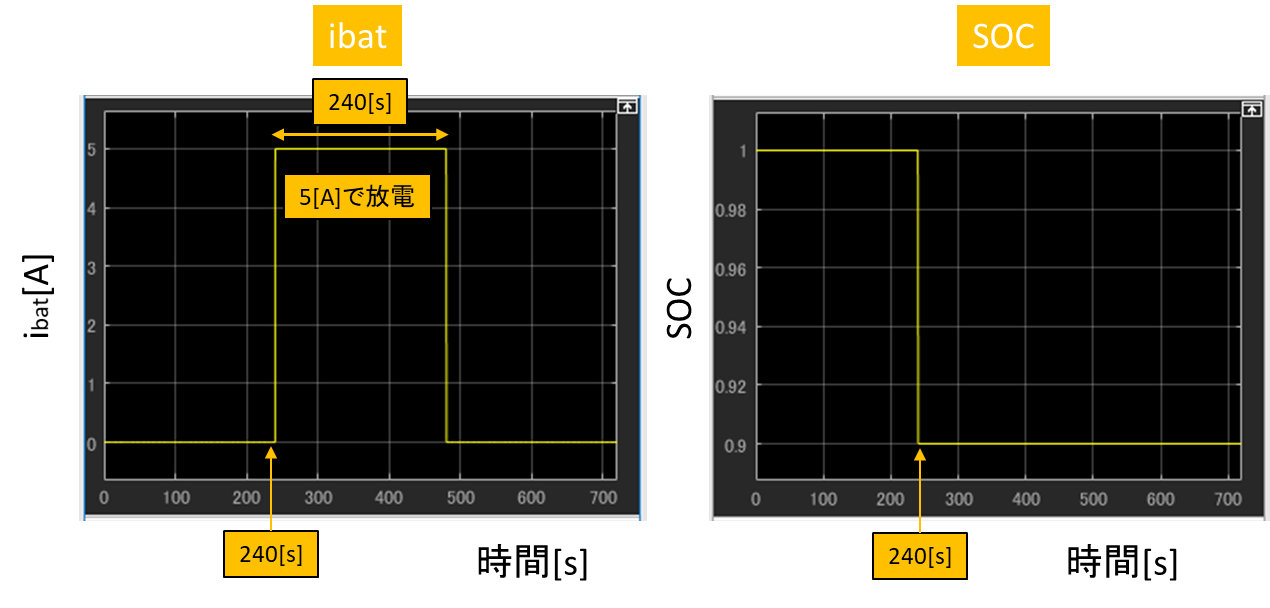
図9 評価条件(ibat,SOC)
※画像クリックで大きな画像が表示されます。
バッテリの端子電圧Vbatのシミュレーション結果は図10の通りです。5[A]の放電電流ibatが流れ始める240[s]で変化が現れ、SOCの1→0.9の変化によるEocvの低下とV0(= R0 ibat:前回ブログの回路方程式①)による電圧降下、V1(=(1/C1)∫ (ibat – V1/ R1)dτ:前回ブログの回路方程式⑦)による電圧降下でVbatが変化します。V1の電圧降下の特性はR1とC1のカップリングできまります。放電電流がきれる480[s]でV0成分の電圧降下がなくなり、その後緩やかにV1成分の電圧降下分がなくなり、SOCが0.9の時のEocvに収束していきます。
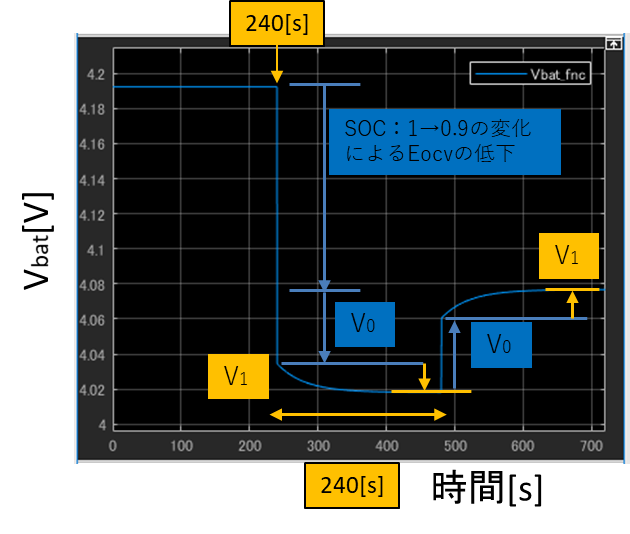
図10 Vbatのシミュレーション結果
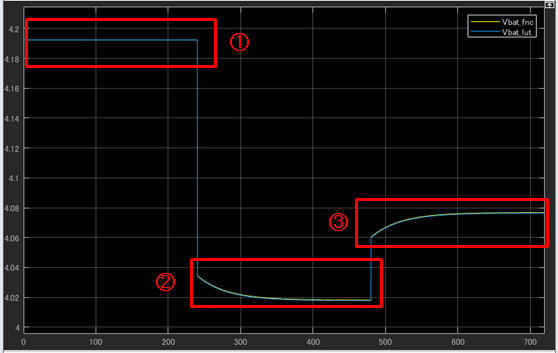
図11 Vbatのシミュレーション結果(fnc vs lut)
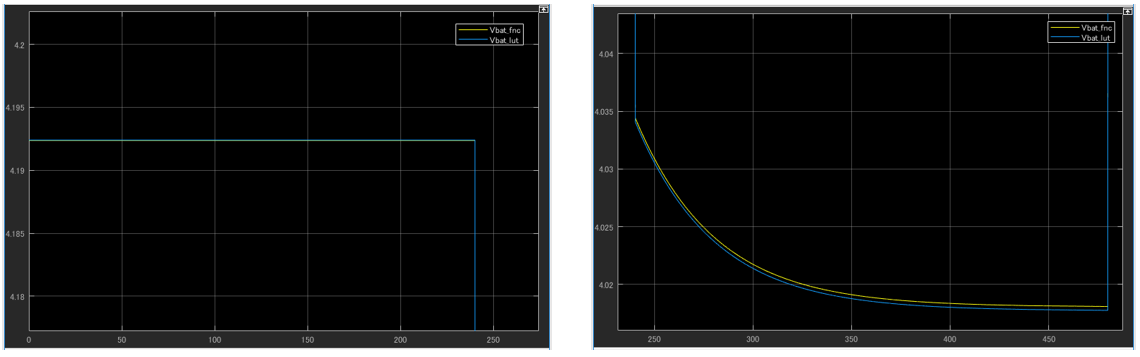
図12 ①の拡大
図13 ②の拡大
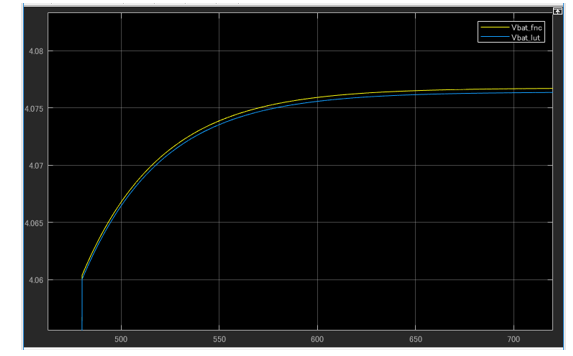
図14 ③の拡大
第2回のLookup Tableを使用したモデルのVbatのシミュレーション結果と比較したものが図11~図14です。黄色が近似式の結果、青色がLookup Tableでの結果です。この結果から近似式がLookup Tableをよく近似できていることが分かります。
終わりに
今回はリチウムイオンバッテリのSimulink®モデルを、SOC(充電率)を変数とする近似式でOCV電圧、R、Cを表現するモデルを作成しました。
近似式の算出に際しては、高次(最高10次)の多項式にも対応する、「MATLAB の基本的な近似 UI 」を使用しました。
SOCが1の状態からibat =5[A]で240[s]間放電し、SOCが0.9となる場合のVbatの変化をシミュレーションにより確認しました。前回のLookup Tableを使用したモデルとシミュレーション結果を比較し、よく近似できていることが確認できました。
もしお手元にあるSimulink®モデルのHDL化やモデルベースデザイン設計を委託したいというご要望がございましたら、以下よりお気軽にお問い合わせください。
最後までお付き合いいただきありがとうございました。