マス・バネ・ダンパモデルをSimulink®で作ってみた

このブログでは、自動車業界で普及してきている「モデルベース設計」を用いて、様々な物理現象をモデル化します。今回はマス・バネ・ダンパをモデル化します。
このモデル作成は、物理モデルから微分方程式を導き、それを元にMathWorks社のSimulink®を使用してモデルを作成しており、シミュレーションによる評価を行う一連の流れを紹介します。
なお、実行した環境は以下の通りです。
| OS | Microsoft Windows 10 Pro |
|---|---|
| MathWorks社製 | MATLAB® バージョン 9.9 (R2020b) |
| Simulink® バージョン 10.2 (R2020b) |
目次
マス・バネ・ダンパの物理モデル
マス・バネ・ダンパの物理モデルを図 1に示します。
バネ、ダンパにつながる質量M[kg]の物体に外力f(t)[N]が加わったときの時刻t[s]における変位x(t)[m]をモデル化しています。
バネの自然長となる位置を基準位置0[m]とします。
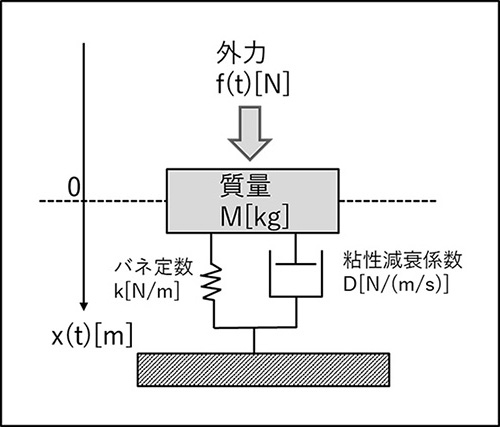
図1 マス・バネ・ダンパの物理モデル
時間変動する物理量は以下の通りです。
また、パラメータは以下です。
物理モデルを微分方程式へ
図 1の物理モデルを微分方程式にしたものを以下に示します。
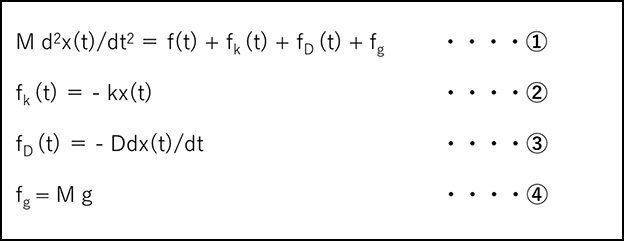
それぞれの式の意味は以下の通りです。
- ① バネの復元力fk (t)[N]、ダンパ制動力fD (t)[N]、物体に働く重力fg[N]としたときの並進運動の運動方程式
- ② バネ定数k[N/m]を用いてフックの法則から求めたバネの復元力fk (t) [N]
- ③ 粘性減衰係数D[N/(m/s)]を用いて速度に比例する、ダンパの制動力fD (t)[N]を表現
- ④ 重力加速度g[m2/s]を用いて重力fgを表現
微分方程式をSimulink®モデルへ
外力f(t)[N]を入力、物体の変位x(t)[m]を出力とするSimulink®モデルを作成します。

作成したものが、図 2のモデルです。
なお、変位の初期条件として、重力とバネの復元力fk (t)[N]が釣り合う
Mg – k x(0) = 0
∴x(0)=M*g/k
を設定しました。
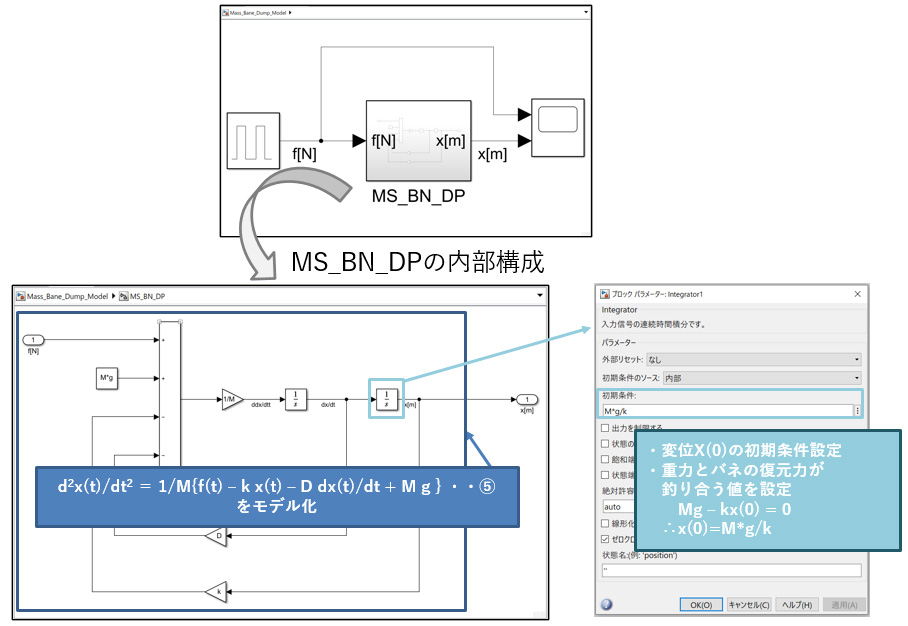
図2 マス・バネ・ダンパのSimulink®モデル
シミュレーションによる評価
上記のモデルに以下図 3のパラメータを設定して、図 4入力のようにマス・バネ・ダンパモデルで時刻t=15[s]に外力f(t)=10[N]をステップ入力で与えて、シミュレーション実行して変位x(t)を評価しました。
シミュレーション結果は図 4の通りです。
外力を加える前は、重力とバネの復元力fk (t)[N]が釣り合う、変位x=9.8[m]で、外力が加わるとともに増加し始め最大約10.96[m]になることが分かります。
時刻t=30[s]で外力を無くすと変位は減少し始め、最終的には外力を加える前の元の変位x=9.8[m]に収束していきます。
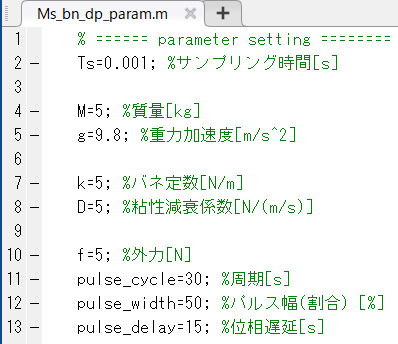
図3 設定パラメータ
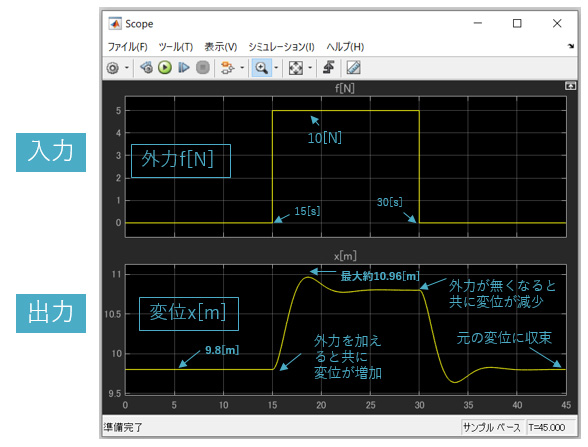
図4 マス・バネ・ダンパモデルのシミュレーションの様子
おわりに
今回は「マス・バネ・ダンパモデルの変位」について、物理モデルから微分方程式を導き、それを元にMathWorks社のSimulink®を使用してモデルを作成しました。
変位の初期条件を重力と復元力が釣り合う平衡状態とし、変位の経時変化の様子をシミュレーションで確認しました。
モデルベースデザイン設計委託やお手元にあるSimulink®モデルのHDL化のご要望がございましたら、弊社デザインサービス事業までお気軽にお問い合わせください。
最後までお付き合いいただきありがとうございました。
参考文献[1]:山本透 他, “実習で学ぶモデルベース開発”,コロナ社 (2018)















